Find missing number in an array | Leetcode 268 | Explained

Here’s Leetcode 268 – Missing Number, a classic array and number theory problem [Problem Link]. We will go through it step by step and see the most efficient way to solve it with optimal time and space complexity. We will also do a dry run with multiple examples so you can see how it works in practice.

By the end of this you will know the Missing Number problem and be able to implement the solution efficiently. So let’s get started!

Understand the problem

You are given an array of n unique integers where each number is in the range [0, n]. The array is missing exactly one number within this range, and your task is to find that missing number.

Example 1

• Input: nums = [3, 0, 1]
• Range: [0, 3]

Here, the sequence should have contained 0, 1, 2, 3, but 2 is not present in nums. So the missing number is 2.

Example 2

• Input: nums = [0, 1]
• Range: [0, 2]

This array contains 0 and 1, but is missing 2. So the missing number is 2.

Example 3

• Input: nums = [9, 6, 4, 2, 3, 5, 7, 0, 1]
• Range: [0, 9]

Every number from 0 to 9 should appear exactly once, but in this list, 8 is nowhere to be found. Therefore, the missing number is 8.

Also read about a DSA Problem on – Count the Maximum Consecutive One’s.

Brute Force Solution

How do we solve?

The approach is simple:

1. We know the missing number has to be an integer in 0 to n.
2. We check sequentially from i = 0 to i = n if i is not in the list nums.
3. When we find such an i, we return it because it must be the missing number.

This is correct because:

• We are checking 0 to n, so we cover all numbers in the range.
• First number not found in nums is by definition the missing one.

Code Implementation

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        for i in range(0, len(nums) + 1):
            if i not in nums:
                return i

Step-by-Step Explanation

1. Loop Through Possible Numbers: Go from i = 0 to i = len(nums) (inclusive).
2. Check Membership: For each i, we check if i is not in the list nums.
3. Return If Absent: The moment we find i that doesn’t exist in nums, we return i as the missing number.

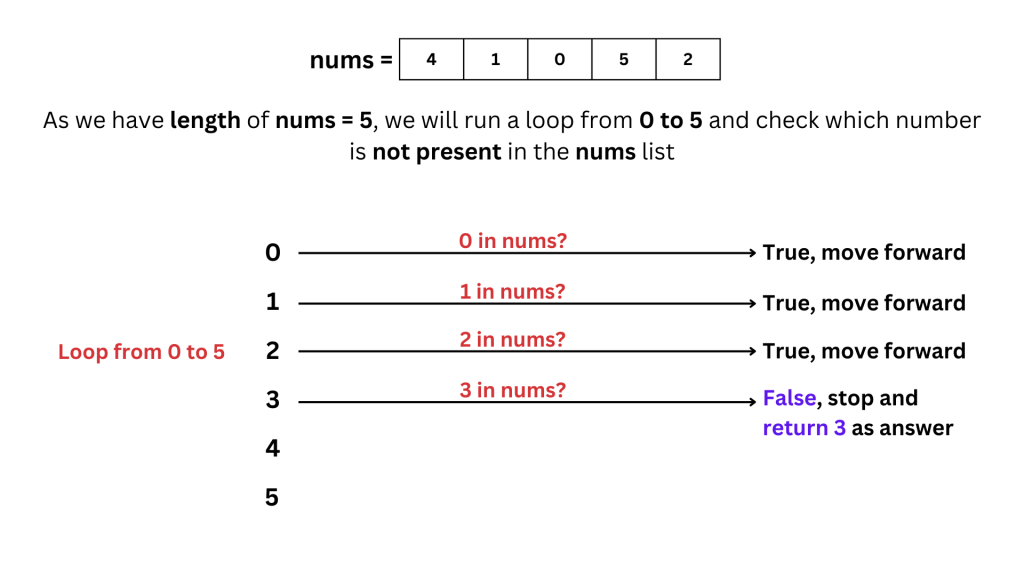
Dry Run

Let’s go through the code step by step, using images to illustrate the detailed dry run process.

Potential Edge Cases

1. Smallest Array:
   • If nums = [1] (n = 1), the missing number might be 0.
2. All Elements Present Except the Last:
   • If nums = [0, 1, 2, …, n-1], then the missing number is n.
3. Missing 0:
   • If nums = [1, 2, 3, …, n], return 0.
4. Already In Order:
   • Even if nums is sorted [0, 1, 2, 3, …, m-1, m+1, …, n], our logic still checks each number.

Time and Space Complexity

1. Time Complexity:O(n^2) in the worst case because:
   • We are looping from 0 to n (which is n+1 iterations).
   • Each membership check (i not in nums) is O(n) for a list.
2. Space Complexity: O(1), as we only use extra variables for iterating (i) and do not allocate significant extra space.

Better Solution (Using Dictionary)

Intuition and Approach

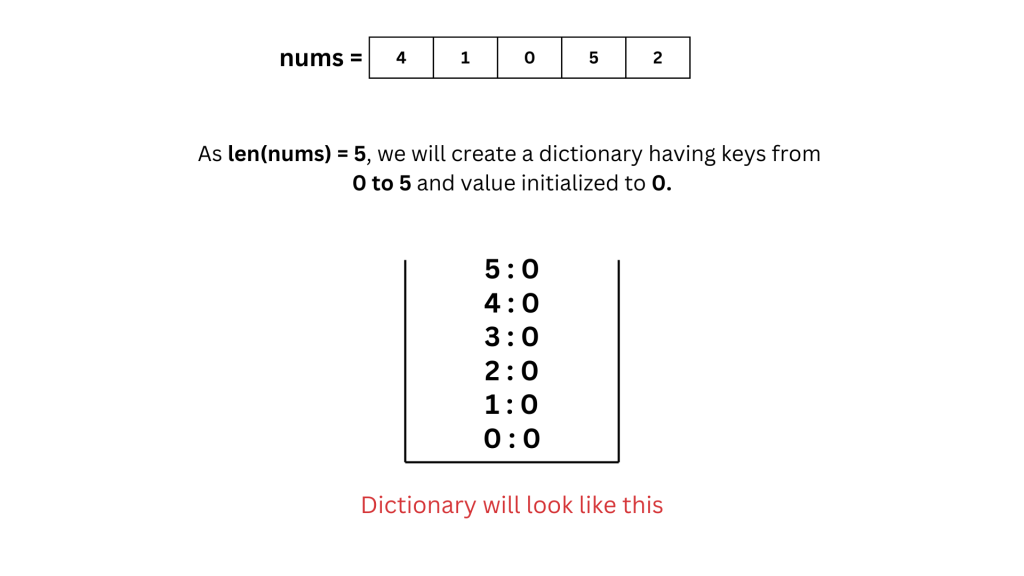
Our approach uses a frequency map (dictionary) to keep track of which numbers appear in the array:

1. Create a dictionary freq where each key in the range [0 … n] is initialized to 0.
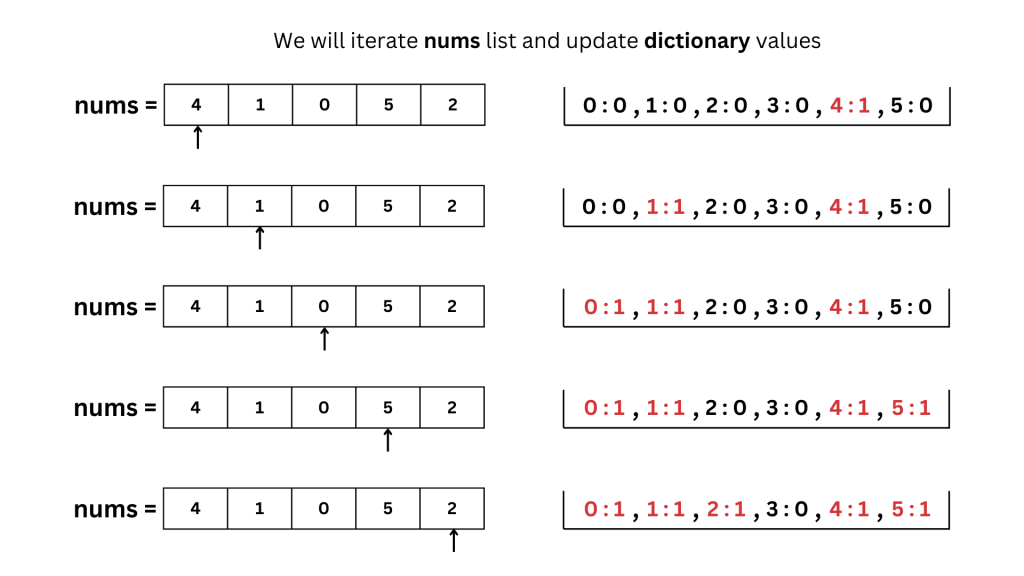
2. Iterate over the elements of nums and increment the corresponding value in freq.
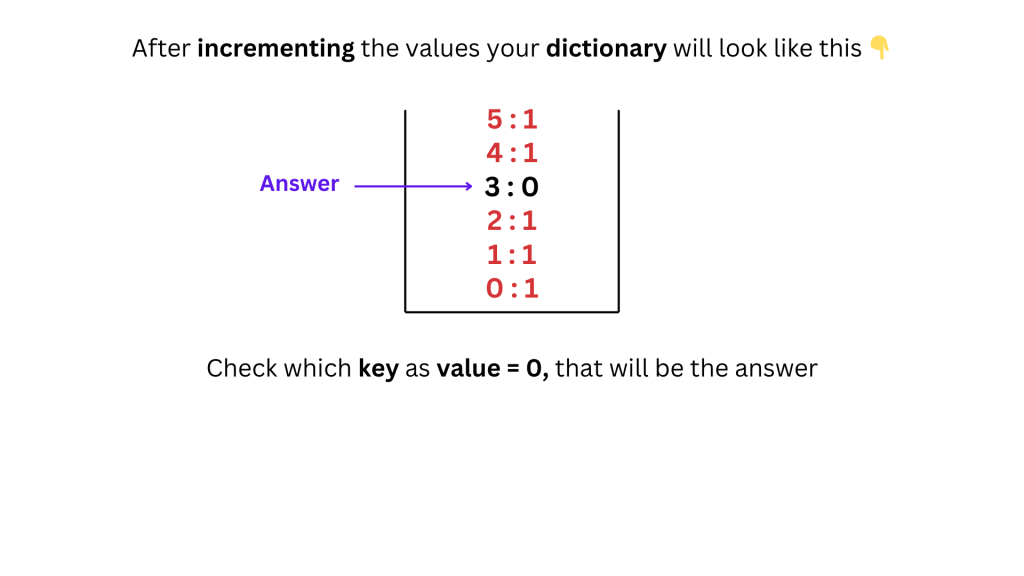
3. Finally, check which key in freq remains at 0, meaning that number never appeared in nums. Return this key.

By doing so, we ensured every number that appears in nums is marked. The one that remains at a 0 is the missing number.

Code

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        freq = {i: 0 for i in range(0, len(nums) + 1)}
        for i in nums:
            freq[i] += 1
        for k, v in freq.items():
            if v == 0:
                return k

Step-by-Step Explanation

1. Create a dictionary freq with keys from 0 up to len(nums) (inclusive), each set to 0.
2. Traverse the list nums and increment freq[i] for each number i in nums.
3. Iterate over each key-value pair in freq. The first key (k) whose value (v) is 0 is the missing number, so return k.

Dry Run

Let’s go through the code step by step, using images to illustrate the detailed dry run process.

Edge Cases

1. Smallest Array:
   • If nums = [1] (which means n = 1), the missing number is 0.
2. All Elements Present Except the Last:
   • If nums = [0, 1, 2, …, n-1], the missing number is n.
3. Missing 0:
   • If nums = [1, 2, 3, …, n], return 0.
4. Already In Order:
   • If nums is sorted [0, 1, 2, …, m-1, m+1, …, n], the dictionary will still capture the missing number.

Time and Space Complexity

• Time Complexity: O(n) to populate freq plus another O(n) to iterate over its items, which simplifies to O(2n) = O(n).
• Space Complexity: O(n) because we create a dictionary of size n+1.

Optimal Solution

Intuition and Approach

We use the formula for the sum of the first n natural numbers:

1. We know the sum of all numbers from 0 to n is:
   n × (n+1) / 2​
2. So if we calculate the expected sum and then subtract the actual sum of the elements in nums, the difference will be the missing number.

This is a sneaky trick because we don’t check each element individually, we just use simple arithmetic.

Code

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        n = len(nums)
        original_total = (n * (n + 1)) // 2
        return original_total - sum(nums)

Step by Step Explanation

1. Calculate n as the length of nums.
2. Calculate the expected sum of all numbers from 0 to n using the formula:
   (n x (n + 1)) // 2
3. Calculate the actual sum of elements in nums using sum(nums).
4. Subtract the actual sum from the expected sum to get the missing number.

Dry Run

Example: Suppose nums = [3, 0, 1].

• n = 3, so the numbers should be {0, 1, 2, 3}.
• Using the formula: total = (n x (n + 1)) // 2 = 6
• The actual sum of nums is 3 + 0 + 1 = 4.
• The missing number is 6 – 4 = 2.

So the function returns 2.

Time and Space Complexity

• Time Complexity: O(n) to calculate sum(nums). The arithmetic operations themselves are O(1).
• Space Complexity: O(1), since we only store a few numeric variables.

For any changes to the article, kindly email at code@codeanddebug.in or contact us at +91-9712928220.