Move Zeros to end of Array| Explained with Images | Leetcode 283

In this article we’ll guide you through the program to Move Zeros to End of Array (in place) [Problem Link]. We will see brute force and optimal solution and also the dry run with images to understand the solution properly. So let’s begin.

Understand the problem

You are given an array of integers. Your task is to move all the zeroes in the array to the end, while keeping the order of the non-zero elements. You must do this in-place, meaning you can’t use an additional data structure to return your answer.

Examples

Example 1

• Input: [0, 1, 0, 3, 12]
• Output: [1, 3, 12, 0, 0]

In this example:

• The non-zero numbers 1, 3, and 12 keep their relative order.
• The two zeros get moved to the end.

Example 2

• Input: [2, 0, 4, 6, 0, 7]
• Output: [2, 4, 6, 7, 0, 0]

Here, the zeros were originally in positions 1 and 4 (0-based indexing). After rearranging, all zeroes are at the end, while 2, 4, 6, and 7 maintain their original order relative to each other.

Example 3

• Input: [0, 0, 1]
• Output: [1, 0, 0]

Even if there are consecutive zeroes at the front, they should end up together at the back once you’ve moved them.

Also read about the Python Program to Implementation of Linear Search in Python.

Brute Force Solution

Our main focus will be storing all the non-zeros elements in a seperate list/array and then change the first elements in original array with those numbers. We won’t be actually moving any zeros, but just replacing it. Let’s see how can we do this.

Intuition and Approach

The approach taken involves separating the non-zero elements from the zeros so that it makes us easy to rearrange the elements afterwards:

1. Iterate the array and copy all non-zero elements into a temporary list called temp.
2. Replace the beginning of the original array with the elements of temp, thus moving all non-zero elements to the front.
3. Fill the remanining of the array with zeros, starting from the index where the non-zero elements end.

This method makes sure that non-zero elements maintain their original sequence, and all zeros are pushed to the end of the array.

Code

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        n = len(nums)
        temp = []

        # Copy non-zero elements from original to temp array
        for i in range(n):
            if nums[i] != 0:
                temp.append(nums[i])

        # Number of non-zero elements
        nz = len(temp)

        # Copy elements from temp to fill first nz fields of original array
        for i in range(nz):
            nums[i] = temp[i]

        # Fill the rest of the cells with 0
        for i in range(nz, n):
            nums[i] = 0

Code Explanation (Stey by Step)

1. Initialize a temp variable:
   • A temporary list temp is created to store non-zero elements found during the iteration of nums.
2. Extract Non-Zero Elements:
   • The array nums is traversed, and each non-zero element is appended to temp.
3. Refill Original Array with Non-Zero Elements:
   • The length of temp, stored in nz, indicates the number of non-zero elements.
   • The first nz positions of nums are overwritten with the elements from temp, placing all non-zero elements at the start of nums.
4. Fill Remaining Positions with Zeros:
   • The remainder of the array from index nz to n (length of nums) is filled with zeros, moving all zeros to the end of the array.

Dry Run (with images)

Let’s go through the code step by step, using images to see the detailed dry run process.

Edge cases to consider

• All Zeros: If nums contains only zeros (e.g., nums = [0, 0, 0]), our code will run as expected and won’t throw any error.
• No Zeros: If there are no zeros (e.g., nums = [1, 2, 3]), nums remains unchanged after the operation, as expected.
• Empty Array: If nums is empty, our code should handle this by performing no operations.

Time and Space Complexity Analysis

• Time Complexity: The complexity is O(2n) due to three separate traversals of the array (n is the length of nums): one to fill temp, one to copy non-zeros back, and one to add zeros.
• Space Complexity: The space complexity is O(n) for the temporary list temp, which in the worst case (no zeros) stores a copy of all elements from nums.

Optimal Solution (Using Two Pointers)

We will be using two pointers named as i and j, to solve this solution. Have a look below and you will understand why this solution works and why this is optimal.

Intuition and Approach

The approach used here is the two-pointer technique to efficiently separate zero and non-zero elements:

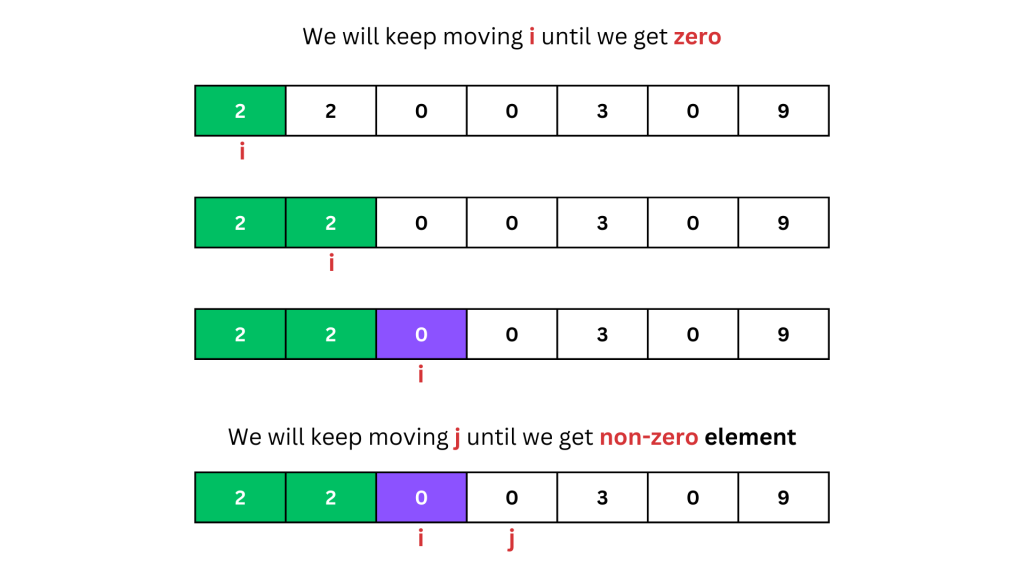
1. The first pointer, i, is used to find the first zero in the array.
2. The second pointer, j, starts from i + 1 and is used to find the next non-zero element to swap with the zero at index i.
3. This process continues, incrementally moving the i pointer each time a swap is made, effectively “collecting” non-zero elements at the start of the array and pushing zeros to the end.

This method makes sure that the operations are done in-place, and by avoiding the use of extra storage or multiple passes, it optimizes both space and time efficiency.

Code

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        if len(nums) == 1:
            return
        i = 0
        while i < len(nums):
            if nums[i] == 0:
                break
            i += 1
        else:
            return
        j = i + 1
        while j < len(nums):
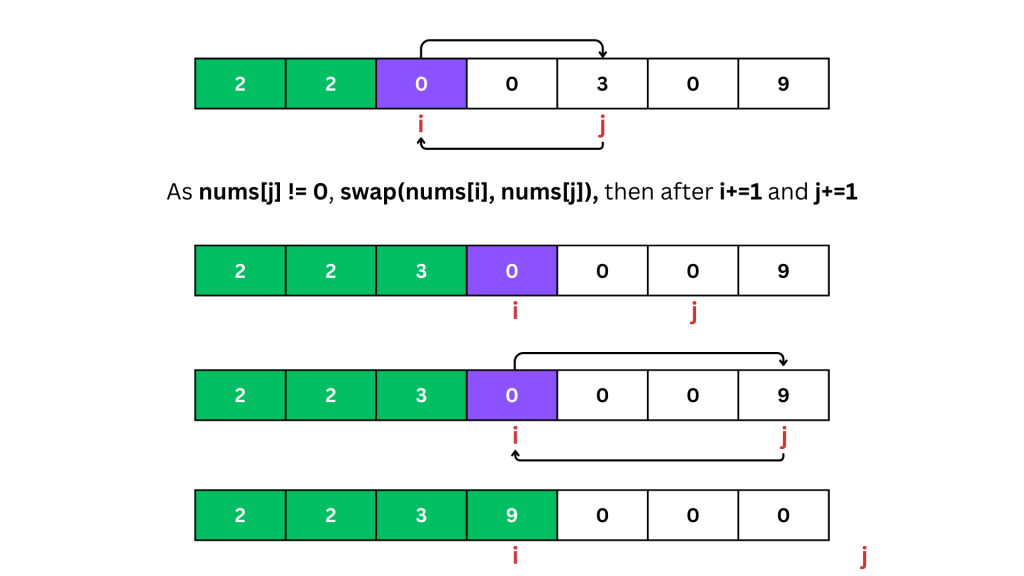
            if nums[j] != 0:
                nums[i], nums[j] = nums[j], nums[i]
                i += 1
            j += 1

Code Explanation (Step by Step)

1. Initial Checks:
   • If the array contains only one element, no action is needed, our code returns immediately.
2. Find First Zero:
   • The i pointer is used to find the first zero in the array. If no zero is found and i reaches the end of the array, our code exits as no zeros need moving.
3. Rearranging Elements:
   • The j pointer starts from the next index after i and scans for non-zero elements.
   • When a non-zero element is found, it is swapped with the zero at the i index. After the swap, i is incremented to point to the next zero, ready for a future swap.
   • This process continues until j has reached to the end of the array.

Dry Run (with images)

Let’s go through the code step by step, using images to see the detailed dry run process.

Edge cases to consider

• All Zeros: If nums contains only zeros (e.g., nums = [0, 0, 0]), the array remains unchanged, and the code handles it efficiently.
• No Zeros: If there are no zeros (e.g., nums = [1, 2, 3]), our code stops early after the initial scan, leaving the array unchanged.
• Empty Array: If nums is empty, the function does nothing, as expected.
• Single Element: A single element (whether zero or non-zero) needs nothing to be done, as handled by the initial return.

Time and Space Complexity Analysis

• Time Complexity: The complexity is O(n), where n is the length of the array. Each element is considered at most once by the j pointer.
• Space Complexity: The complexity is O(1) as the solution modifies the array in place without using additional storage.

Efficiency: This method is space-efficient due to its in-place operation and time-efficient due to its linear complexity. By directly moving non-zero elements forward and letting zeros fill the remaining indices, it maintains the order of non-zero elements without additional data structures.

For any changes to the document, kindly email at code@codeanddebug.in or contact us at +91-9712928220.